70以上 (a+b)^3 formula expansion 328967-(a+b)^3 formula expansion
A B C 3 Formula Source(s) https//shrinkurlim/badse 0 0 DanielM Lv 4 1 decade ago This is just multiplying out and bookkeeping It's a^3 b^3 c^3 plus 3 of each term having one variable and another one squared like ab^2, b^2c, all 6 combinations of those, then plus 6abc and that's it 0 5= and so the power series expansion agrees with the Taylor series Thus a function is analytic in an open disk centred at b if and only if its Taylor series converges to the value of the function at each point of the diskLearn how to derive the expansion of $(xa)(xb)$ formula geometrically by the areas of rectangle and square in geometry Learn Proof Latest Math Topics Dec 22, Learn cosine of angle difference identity Nov 18, Learn constant property of a circle with examples Oct 21,
Expanding Logarithms Chilimath
(a+b)^3 formula expansion
(a+b)^3 formula expansion-Expansion The cube of difference between any two terms is expanded as the subtraction of three times the product of both terms and the subtraction of the second term from the first term, from the subtraction of the cube of the second term from the cube of the first term $\implies$ $(ab)^3$ $\,=\,$ $a^3b^33ab(ab)$ SimplificationThe 7th row of Pascal's triangle is 1, 6, 15, , 15, 6, 1, which are the absolute values of the coefficients you are looking for, but the signs will be alternating (ab)^6 = a^6 6a^5b 15a^4b^2 a^3b^3 15a^2b^4 6ab^5 b^6 Compare with the 'positive' case (ab)^6 = a^6 6a^5b 15a^4b^2 a^3b^3 15a^2b^4 6ab^5 b^6 For the 'negative' case, we replace b with b and notice


Factorials To Binomial Theorem
3 Mid point formula 1 2 1 2 x x y y, 2 2 4 Centriod formula 1 2 3 1 2 3 x x x y y y, 3 3 5 Area of triangle when their vertices are given,Introduction to a minus b whole cube identity with example problems and proofs to learn how to derive ab whole cube formula in mathematics1 4 6 4 1
For the sum of cubes, the "minus" sign goes in the quadratic factor, a 2 – ab b 2Related Topics Mathematics Mathematical rules and laws numbers, areas, volumes, exponents, trigonometric functions and more ;Get the list of basic algebra formulas in Maths at BYJU'S Stay tuned with BYJU'S to get all the important formulas in various chapters like trigonometry, probability and so on
Introduction to a plus b whole cube formula with example problems with proofs to learn how to derive ab whole cube identity in mathematicsExercise 3 Expand the following expression, writing your answer in its simplest form Be careful of notation and do not use spaces in your answer ( x ) 2 = x 2 x= (a b)(a b)(a b) = (a b)(a² ab ab b²) = (a b)(a² 2ab b²) = a³ 2a²b ab² a²b 2ab² b³ = a³ 3a²b 3ab² b³


What Is The Formula For Math A 3 B 3 Math Quora


Expanding Logarithms Chilimath
A Plus B Plus C Whole cube Are you looking for A plus B plus C Whole cube?In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive integer dependingWhat Is The Expansion Of A B C 3 Quora For more information and source, see on this link https//wwwquoracom/Whatistheexpansionofabc3


2



A B N And A B N Formula Expander
Discrete Data Sets Mean, Median and Mode Values Calculate arithmetic meanThen notice that each formula has only one "minus" sign The distinction between the two formulas is in the location of that one "minus" sign For the difference of cubes, the "minus" sign goes in the linear factor, a – b;Binomial Theorem – Explanation & Examples A polynomial is an algebraic expression made up of two or more terms which are subtracted, added or multiplied A polynomial can contain coefficients, variables, exponents, constants and operators such addition and subtraction There are three types of polynomials, namely monomial, binomial and trinomial A monomial is an algebraic



Binomial Expansion Factorial Notation And Pascal S Triangle Studywell


What Is The Formula Of Math A B 3 Math Quora
A 3 b 3 = (a b) (a 2 b 2 − ab) (a b c) 3 = a 3 b 3 c 3 3 (a b) (b c) (c a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abcWrite the formula / expansion for (x a)(x b) (x a)(x b) = x 2 (a b)x ab Substitute 2p for x, 1 for a and 2 for bLet us multiply ab by itself using Polynomial Multiplication (ab) (ab) = a2 2ab b2 Now take that result and multiply by ab again (a 2 2ab b 2 ) (ab) = a3 3a2b 3ab2 b3 And again (a 3 3a 2 b 3ab 2 b 3 ) (ab) = a4 4a3b 6a2b2 4ab3 b4


What Is The Formula Of Math A 3 B 3 Math Quora



I Am Taking A Taylor Series Expansion Of A Function F X I Wish To Expand The Function Around The Value G X Is This Allowable
= a^3 3(a^2)b 3a(b^2) b^3 Once you understand the concepts here you can move on to Binomial Expansions and Pascal's Triangles The above will help you with most expansion you come across(AB) and (AB) nth power formula expander is an online tool for algebraic operation programmed to perform formula expansion for any nvalue or nth power of (AB) and (AB) The concept of (AB)^n and (AB)^n formula expander is used to describe the expression for the given nth value of formulaThe square of difference of terms is used as a formula in mathematics in two cases Expansion The square of difference of the terms is expanded as the subtraction of two times product of two terms from the sum of the squares of the terms $\implies$ $(ab)^2 \,=\, a^2b^22ab$ Simplification
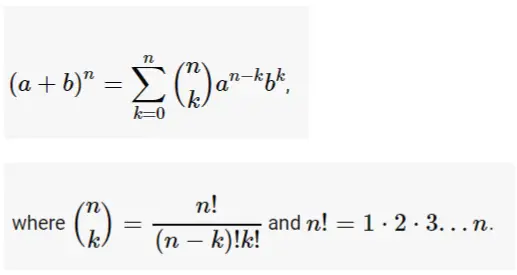


Binomial Expansion Calculator Free Tool To Expand Using Binomial Theorem Onlinecalculator Guru
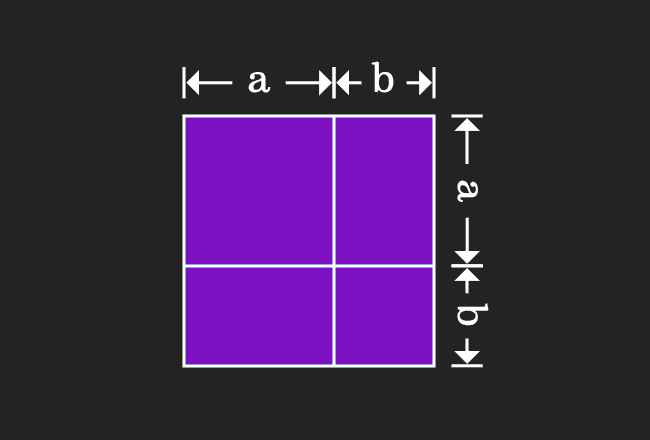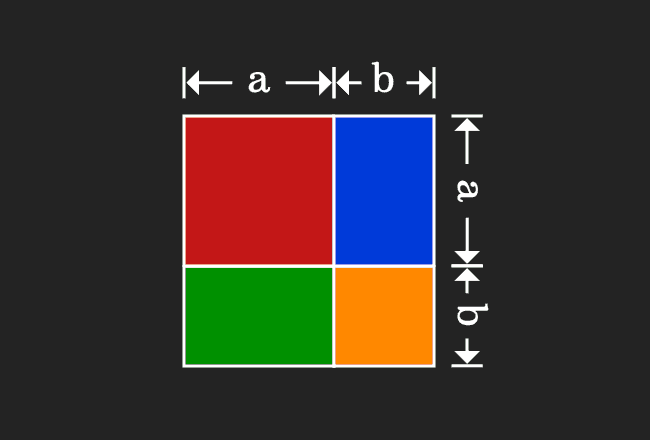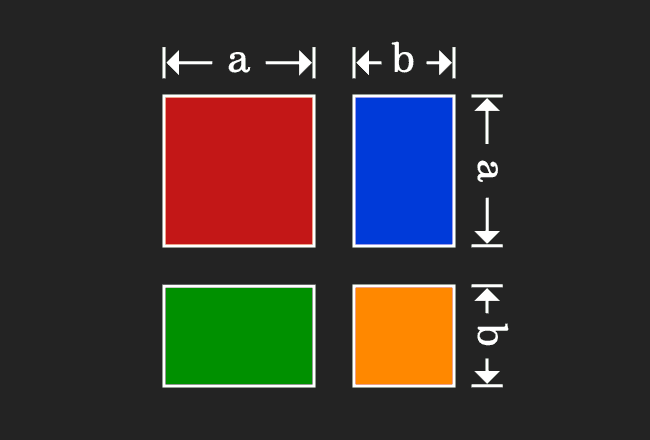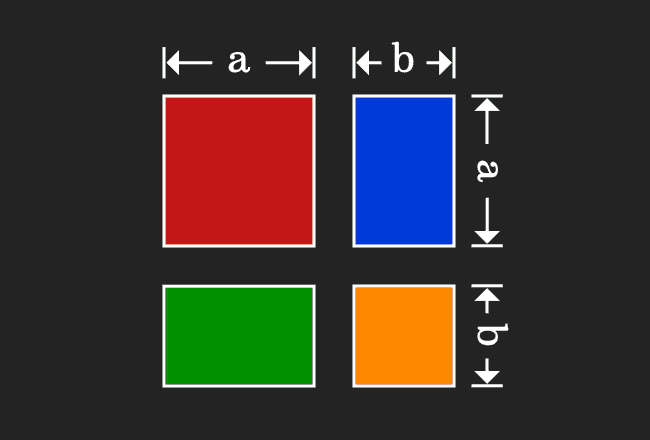


Proof Of A B Formula In Geometric Method
Scalar or pseudoscalar Although the scalar triple product gives the volume of the parallelepiped, it is the signed volume, the sign depending on the orientation of the frame or theIn mathematics, a trinomial expansion is the expansion of a power of a sum of three terms into monomialsThe expansion is given by ( ) = ∑ =,, (,,),where n is a nonnegative integer and the sum is taken over all combinations of nonnegative indices i, j, and k such that i j k = n The trinomial coefficients are given by (,,) =!!!!This formula is a special case of the multinomial(abc) 3 a 3 b 3 c 3 We can choose three "a"'s for the cube in one way C(3,3)=1, or we can choose an a from the first factor and one from the second and one from the third, being the only way to make a3 The coefficient of the cubes is therefore 1 (It's the same for a, b and c, of course) 3a 2 b3a 2 c Next, we consider the a 2 terms We



General And Middle Term Binomial Theorem Formula Videos Examples
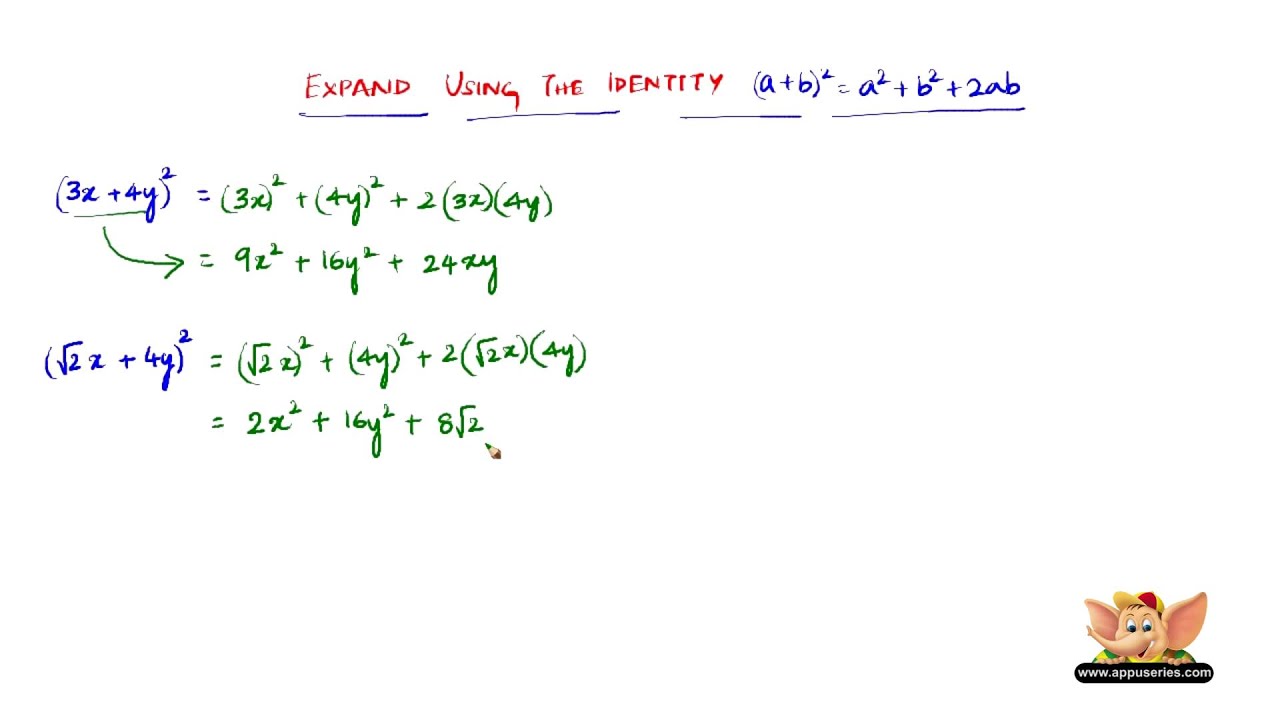


How To Expand Using The Identity A B 2 B2 2ab Youtube
That is, for each term in the expansion, the exponents of the x i must add up to n Also, as with the binomial theorem, quantities of the form x 0 that appear are taken to equal 1 (even when x equals zero) In the case m = 2, this statement reduces to that of the binomial theorem Example The third power of the trinomial a b c is given byThis calculator will solve your problemsQ = (x 2;y 2) you can obtain the following information 1The distance between



11 10 The Binomial Formula Recall A B 2 A 2 2ab B 2 For Any Binomial Expansion A B N There Are N 1 Terms Each Term Is N Th Degree Ppt Download
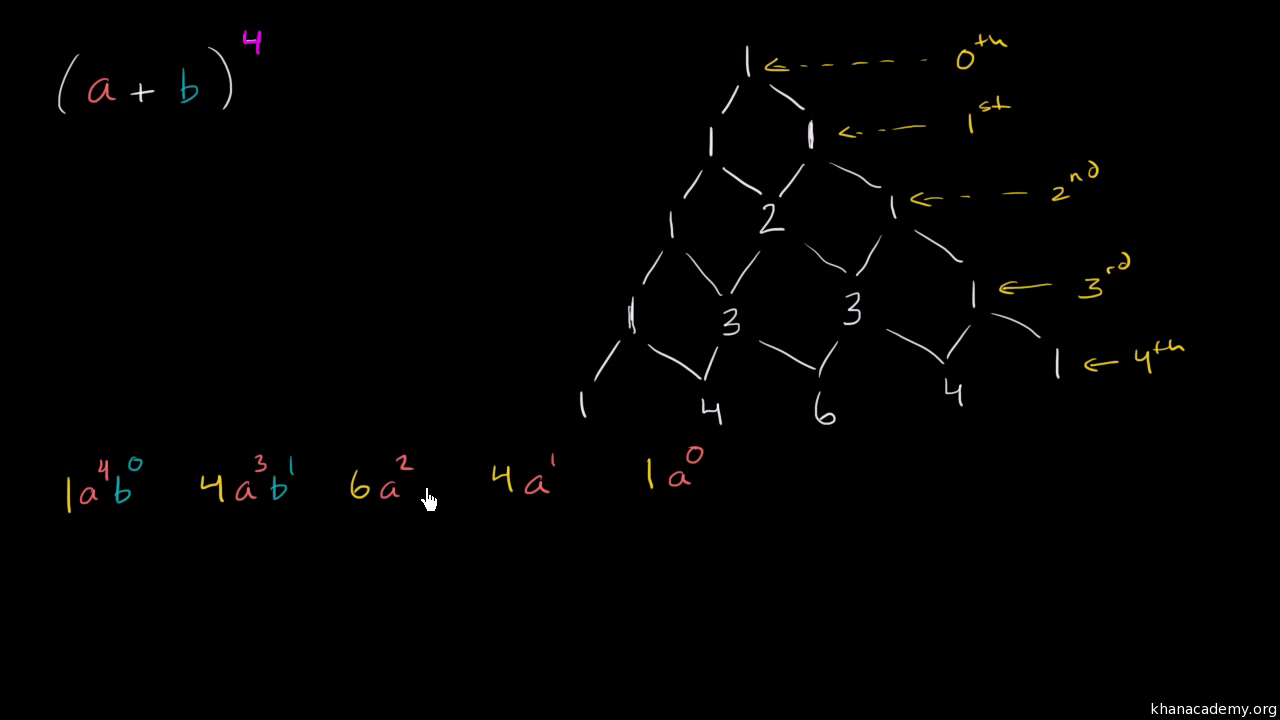


Pascal S Triangle And Binomial Expansion Video Khan Academy
Expansion The cube of the sum of two terms is expanded as the sum of cubes of both terms and three times the product of both terms and sum of them ⟹ (a b) 3 = a 3 b 3 3 a b (a b)This restates in vector notation that the product of the determinants of two 3×3 matrices equals the determinant of their matrix product As a special case, the square of a triple product is a Gram determinant;Differentiating by x the above formula n times, then setting x = b gives ()!


Q Tbn And9gcsjdrnx7bzqtlocyzksajkrzoljxhqicxqu10lfrwznup Pf Ff Usqp Cau



Misc 1 Find A B N In Expansion Of A B N If First Three
What is A3 formula a³ b³ = (a b)(a² – ab b²) you know that (a b)³ = a³ 3ab(a b) b³= and so the power series expansion agrees with the Taylor series Thus a function is analytic in an open disk centred at b if and only if its Taylor series converges to the value of the function at each point of the disk2 29 if a ib=0 wherei= p −1, then a= b=0 30 if a ib= x iy,wherei= p −1, then a= xand b= y 31 The roots of the quadratic equationax2bxc=0;a6= 0 are −b p b2 −4ac 2a The solution set of the equation is (−b p 2a −b− p 2a where = discriminant = b2 −4ac 32



3 Write The Expansion Formula For A B 3



How To Expand A3 Brainly In
Complex Numbers Complex numbers are used in alternating current theory and in mechanical vector analysis;Differentiating by x the above formula n times, then setting x = b gives ()!Quadratic Formula For an equation of the form \(ax^2bxc=0\), you can solve for x using the Quadratic Formula $$ x = \frac{b \pm \sqrt{b^24ac}}{2a} $$ Binomial Theorem \((ab)^1= a b\) \((ab)^2=a^22abb^2\) \((ab)^3=a^33a^2b3ab^2b^3\) \((ab)^4=a^44a^3b6a^2b^24ab^3b^4\) Difference of Squares \(a^2b^2=(ab)(ab)\) Rules of Zero



Algebra Formula Definition Formulas And Examples



Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange
The binomial theorem states a formula for expressing the powers of sums then there is a middle term in the expansion in which the exponents of a and b are the same Only in (a) and (d), there are terms in which the exponents of the factors are the same \right)\left(\frac{a^{3} }{b^{3} } \right)\left(\frac{b^{3} }{a^{3} } \rightExpansion of #(ab)^n# gives us #(n1)# terms which are given by binomial expansion #color(white)x ^nC_ra^((nr))b^r#, where #r# ranges from #n# to #0# Note that powers of #a# and #b# add up to #n# and in the given problem this #n=5# In #(x3y)^5#, we need coefficient of #x^3y^2#, we have #3^(rd)# power of #x# and as such #r=53=2#3 Quadratic Formula Finally, the quadratic formula if a, b and c are real numbers, then the quadratic polynomial equation ax2 bx c = 0 (31) has (either one or two) solutions x = b p b2 4ac 2a (32) 4 Points and Lines Given two points in the plane, P = (x 1;y 1);



How To Develop A Numerical Differentiation Formula Using Taylor Expansion Series Mathematics Stack Exchange



Simple Proof Of A B A 3a B 3ab B A B 3ab A B And A B A 3a B 3ab B A B 3ab A B Youtube
22K views · Answer requested by(abc) 3 a 3 b 3 c 3 We can choose three "a"'s for the cube in one way C(3,3)=1, or we can choose an a from the first factor and one from the second and one from the third, being the only way to make a3 The coefficient of the cubes is therefore 1 (It's the same for a, b and c, of course) 3a 2 b3a 2 c Next, we consider the a 2 terms WeDiscrete Data Sets Mean, Median and Mode Values Calculate arithmetic mean



Binomial Theorem Examples Solutions Examples Videos Worksheets Activities
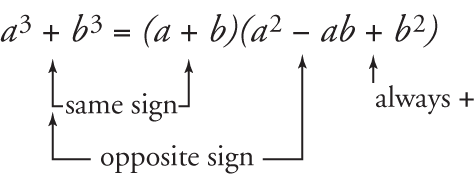


Sum Or Difference Of Cubes
One way to Do this, is to first learn what is (A B) ^3 by just multiplying A B with itself 3 times and you will have (A B)^3 = A^3 3A^2B 3AB^2 B^3 Now replace A by a and B by (b c) and Do the Work !Http//wwwfreemathvideoscom In this video playlist I will show you the basics for polynomial functions We will start with factoring polynomial equationsShows you the stepbystep solutions using the quadratic formula!



What Is The Formula Of Math A B 3 Math Quora



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo
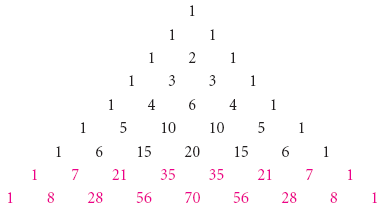
Related Documents Binomial Theorem Binomial theorem for positive integers;To find an expansion for (a b) 8, we complete two more rows of Pascal's triangle Thus the expansion of is (a b) 8 = a 8 8a 7 b 28a 6 b 2 56a 5 b 3 70a 4 b 4 56a 3 b 5 28a 2 b 6 8ab 7 b 8 We can generalize our results as follows The Binomial Theorem Using Pascal's TriangleThe general formula is given by the Binomial Formula where is called the Binomial Coefficient Recall that the factorial of the natural number n is given by Putting the stuff together, we get Note also that we have Factoring Formulas which extends to the general formulas (the second formula only works for odd exponents n) Differential



Binomial Theorem Wikipedia



Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning
Related Documents Binomial Theorem Binomial theorem for positive integers;What is A3 formula a³ b³ = (a b)(a² – ab b²) you know that (a b)³ = a³ 3ab(a b) b³2 29 if a ib=0 wherei= p −1, then a= b=0 30 if a ib= x iy,wherei= p −1, then a= xand b= y 31 The roots of the quadratic equationax2bxc=0;a6= 0 are −b p b2 −4ac 2a The solution set of the equation is (−b p 2a −b− p 2a where = discriminant = b2 −4ac 32



Pascal S Triangle And The Binomial Theorem X Y 0 1 X Y 1 1x 1y X Y 2 1x 2 2xy 1y 2 X Y 3 1x 3 3x 2 Y 3xy 2 1 Y 3 X Ppt Download
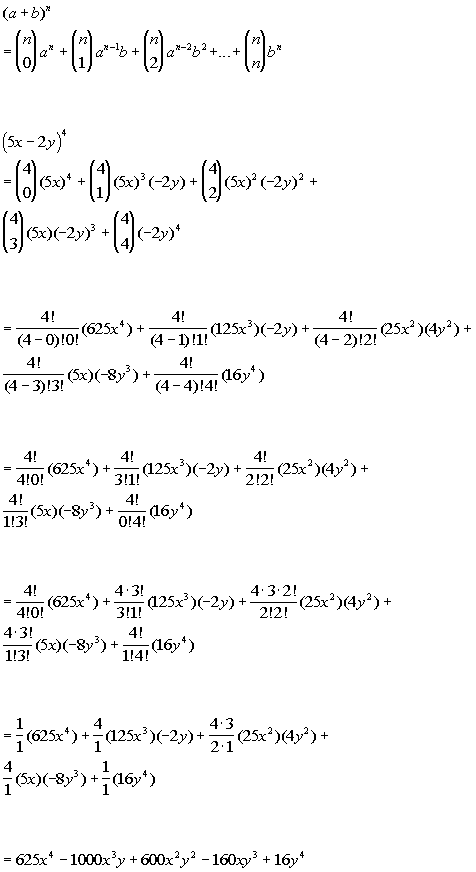


Wtamu Math Tutorials And Help
You can check the formulas of A plus B plus C Whole cube in three ways We are going to share the (abc)^3 algebra formulas for you as well as how to create (abc)^3 and proof weComplex Numbers Complex numbers are used in alternating current theory and in mechanical vector analysis;Write the formula / expansion for (x a)(x b) (x a)(x b) = x 2 (a b)x ab Substitute 2p for x, 1 for a and 2 for b


Mast Queensu Ca Mikeroth Oldteaching Math326 Hmwk Hmwk09 Pdf



Solved 5 Show The Expansion And Evaluate 5 A 3 S 3 K Chegg Com
Basically you need to think of it as (ab) (ab) (ab) because that's what exponents do And then you multiply one of the (ab) parts with another (ab) Repeat with the last (ab) The webpage hasIn using the binomial formula, we let `a = 2x,` `b = 3` and `n = 4` Substituting in the binomial formula, we get `(2x3)^4` `=(2x)^44(2x)^3(3)` `(4(3))/(2!)(2x)^2(3)^2` `(4(3)(2))/(3!)(2x)(3)^3(3)^4` `=16x^496x^3216x^2216x81`The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex roots Calculator determines whether the discriminant \( (b^2 4ac) \) is less than, greater than or equal to 0 When \( b^2 4ac = 0 \) there is one real root When \( b^2 4ac > 0 \) there are two real roots


4 The Binomial Theorem



3 3 Determinants By Expansion Wolfram Demonstrations Project
Related Topics Mathematics Mathematical rules and laws numbers, areas, volumes, exponents, trigonometric functions and more ;To find an expansion for (a b) 8, we complete two more rows of Pascal's triangle Thus the expansion of is (a b) 8 = a 8 8a 7 b 28a 6 b 2 56a 5 b 3 70a 4 b 4 56a 3 b 5 28a 2 b 6 8ab 7 b 8 We can generalize our results as follows The Binomial Theorem Using Pascal's Triangle
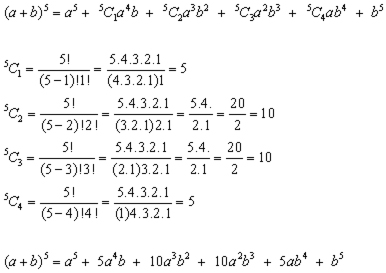


The Binomial Theorem Algebra Pure Mathematics From A Level Maths Tutor
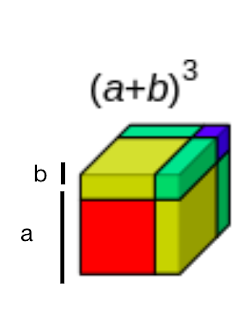


Yismxplusc Geometric Proof Of The Cubic Formula A B 3
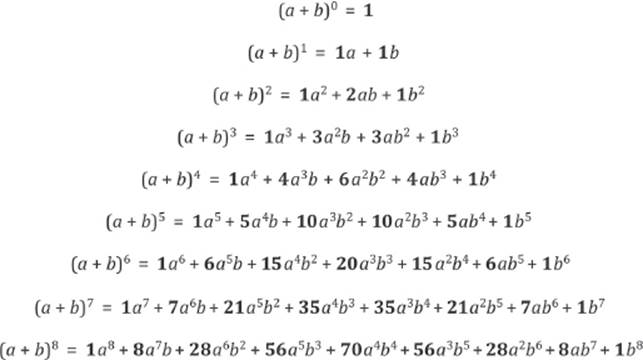


The Binomial Expansion Number Explorations Numbers Their Tales Types And Treasures



What Is A B 3 Quora



Binomial Theorem



Expansion Archives Sat Prep


The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets



Taylor Series Expansion


A 2 B 2



Solved 2 We Ve Studied The Binomial Theorem In Class In Chegg Com



A Cube Plus B Cube Algebra Identity Derivation Youtube



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo
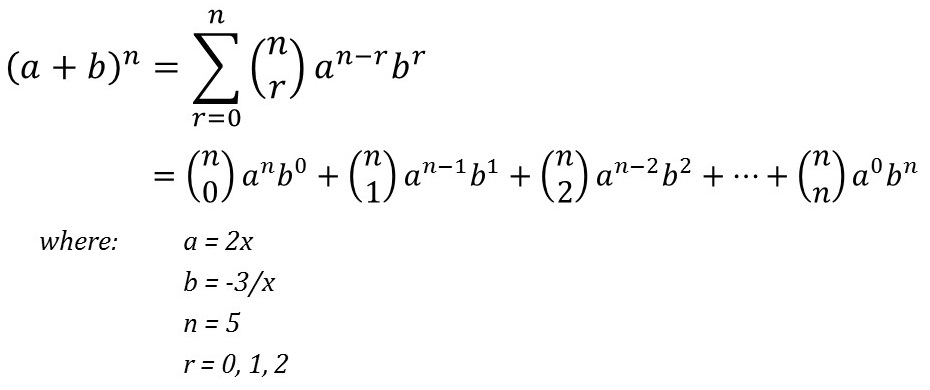


Binomial Expansion Formula A Level



Expanding Algebraic Expressions Using Identities Worksheets



Number Skill Math And Chemistry Tuition Binomial Theorem General Term Formula Facebook


What Is The Expansion Of A B C 3 Quora



Multinomial Expansion
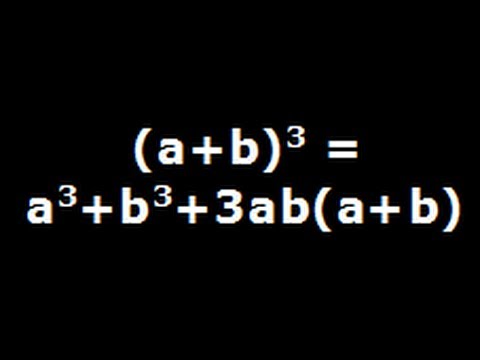


A Plus B Cube Algebra Identity Explained Step By Step Youtube



Binomial Theorem



A B Formula Identity
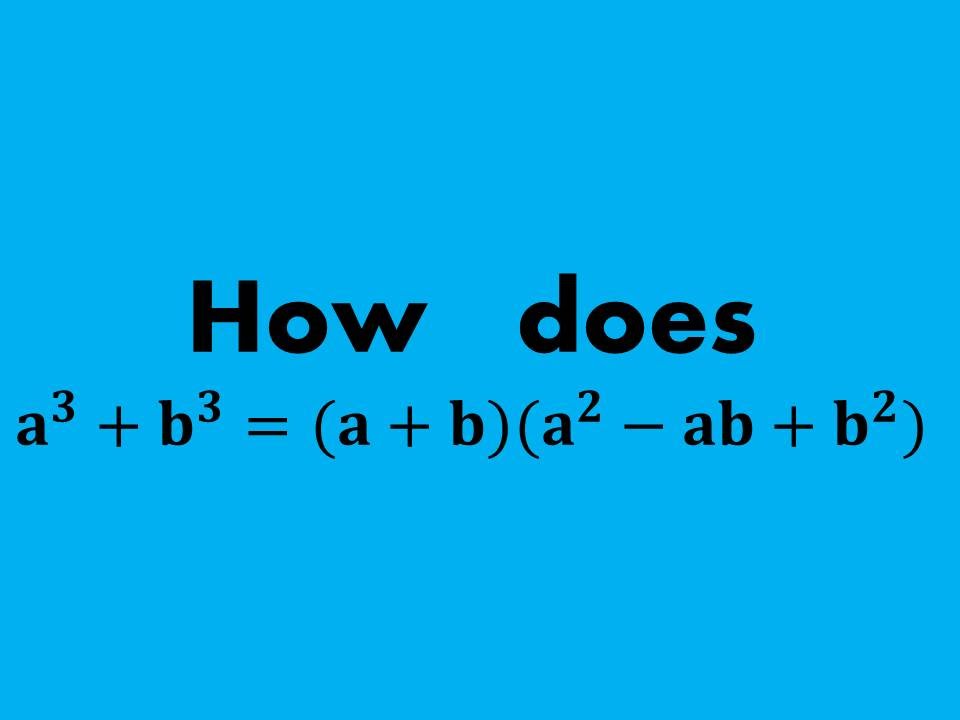


Proof How To Prove The Sum Of Two Cubes A 3 B 3 A B A 2 Ab B 2 Youtube



Expanding Algebraic Expressions Using Identities Worksheets
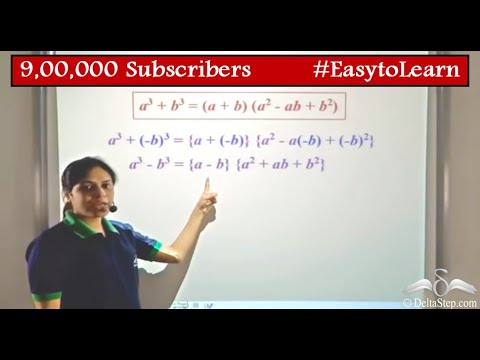


Special Identities A3 A3 Youtube


A B C 3 Formula Expansion



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets



Expanding Algebraic Expressions Using Identities Worksheets



Multinomial Expansion



A B 3 Expansion Formula


Factorials To Binomial Theorem


Factorials To Binomial Theorem


A B C 3 Formula Expansion


Standard Identities Of Binomials And Trinomials Equations Examples



Basic Expansion Of Algebraic Expressions For Children Math Methods Studying Math Algebraic Expressions



Algebraic Identities Standard Algebraic Identities Definition Examples



Solved 3 10 Points A Find A Formula In Terms Of N Chegg Com



Binomial Expansion Using A General Formula Quick Visual Summary With Space For Students To Really Embed T Binomial Theorem This Or That Questions The Expanse


3



Expanding Algebraic Expressions Using Identities Worksheets



The Binomial Theorem A B 2 A B A B 2ab B2 Ppt Video Online Download



Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5


3 Binomial Theorem Ghci Grade 12 Mathematics Of Data Management



Answer Plese All 4 Matching Pair Match The Following 3 Expand A 2 A Va Ctorize Xi 9x Math Expansion Formulae Meritnation Com
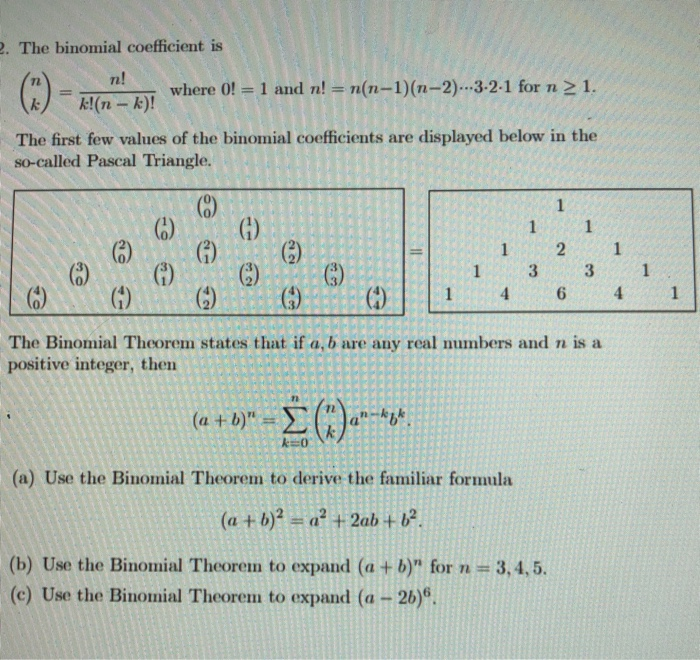


Solved 2 The Binomial Coefficient Is 3 N Where 0 1 Chegg Com



Binomial Theorem Wikipedia


What Is The Formula Of Math A 3 B 3 Math Quora



Pascal S Triangle And The Binomial Theorem


Illustrations Of Formulas



Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab



Expansion Archives Sat Prep


The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium



Msbshse Solutions For Class 8 Maths Part 1 Chapter 5 Expansion Formulae Download For Free



Question Video Finding A Certain Term In A Binomial Expansion



Pascal S Triangle



Binomial Expansion Formula Examples Solutions Worksheets Videos Activities
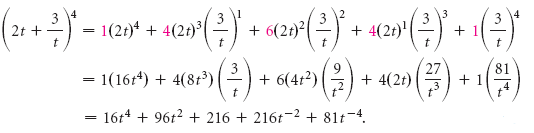


The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets


Q Tbn And9gcrswdldblxmiitn Ggstx6knbcgxw3sex0r673zeswoh Igfkvn Usqp Cau



Intro To The Binomial Theorem Video Khan Academy



A B 3 Expansion Formula


How To Cube Binomials
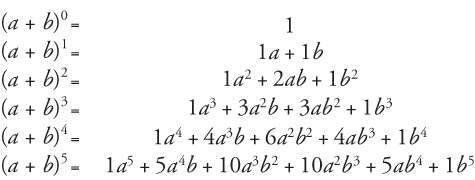


Binomial Coefficients And The Binomial Theorem


Solution Use The Binomial Theorem To Expand The Binomial And Express The Result In Simplified Form X 4 3
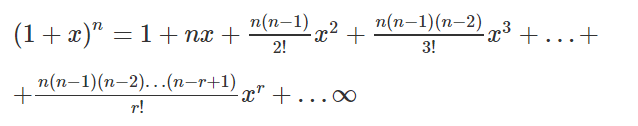


Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf



What Is The Correct Formula Of Math A B 3 Math Quora



What Is The Correct Formula Of Math A B 3 Math Quora



Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf
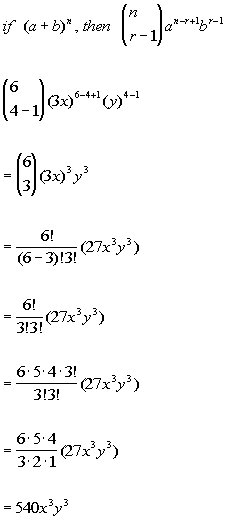


Wtamu Math Tutorials And Help



What Is The Expansion Of A B C 3 Quora


A Level Maths Binomial Expansion The Student Room
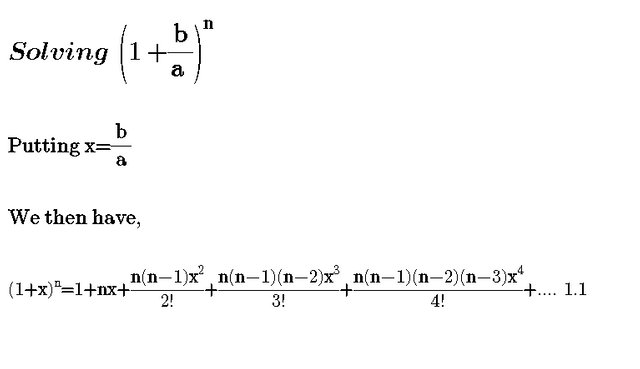


Deriving Of Binomial Expansion Formula For Two Variables A B N Steemit


What Is The Formula Of Math A B 3 Math Quora



コメント
コメントを投稿